Чтож, приветствую всех гвардейцев! Как оказалось, не все понимаю методички и нужно немного пояснений, ну чтож, потому и выходит эта небольшая статейка объясняющая, как решать задачу линейного программирования симплекс методом.
В начале у нас будет дана функция и несколько ограничений на нее:
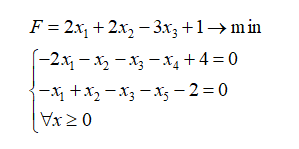
После чего дополняем исходную функцию переменными, которых нет в ней, но есть в системе ограничений, с коэффициентами 0, то есть в нашем случае в функцию пойдет х4 и х5. А так же добавляем две (вообще по количеству ограничений, но не суть важно) дополнительных переменных, например x6 и х7, которые мы так же введем в ограничения. Поскольку у нас задача минимизации, то новые 6-я и 7-я переменные войдут с коэффициентами М (М – число много большее нуля, условно можно считать, что оно стремится к +inf). Если бы у нас была задача максимизации, то мы бы вставили коэффициенты -М.
Так же, в системе ограничений, мы переносим все константы в правую сторону и делаем там, чтобы они были положительными. После чего к левой стороне прибавляем нововведенные x6 и х7.
Сделаем переход:
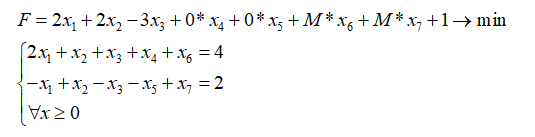
Будь у нас задача максимизации, то первое преобразование было бы таким:
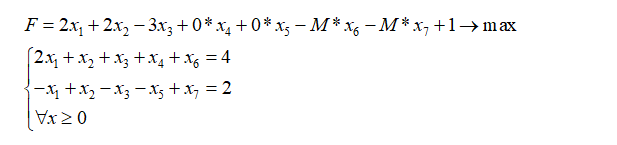
Итак, первый пункт мы выполнили, а именно запись системы ограничений в предпочтительном виде.
Перейдем ко второму пункту – запись и просчет симплекс таблицы. Сначала выпишу ее, после чего объясню что к чему:
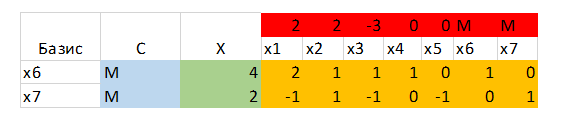
Красную строку мы заполняем коэффициентами из функции F, соответствующие индексам при х
Голубой столбец мы заполняем коэффициентами из функции F членов, то находятся в базисе (столбец левее)
Зеленый столбец мы заполняем свободными членами (константами) из уравнений ограничения
Желтую табличку мы заполняем соответствующими коэффициентами при соответствующих индексам х-сам в предпоследней строке.
Итак, начальную симплекс таблицу мы заполнили, теперь нужно просчитать для нее оценки ∆ и смещения θ. Приведу выкладки, после чего объяснения:
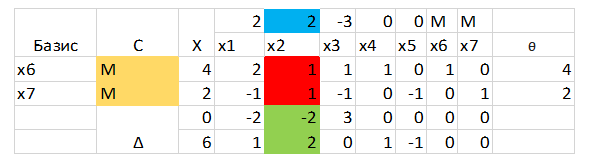
Разберем на примере, как мы считаем оценки: Вектор С*вектор Xj-coef(Xj). Конечно же все всё поняли😉.
А теперь подробнее, в нашем случае оценка дельта это желтый столбец умноженный на соответствующие ему числа из красного и вычтенная из него голубая ячейка: M*1+M*1-2=-2+2*M. После чего в верхнюю строку оценки мы записываем свободный член, тот что без М (то есть -2), а в нижнюю строку коэффициент при М (то есть 2), это можно увидеть в зеленом столбце.
Разберем еще столбик, как считали, например, при х3
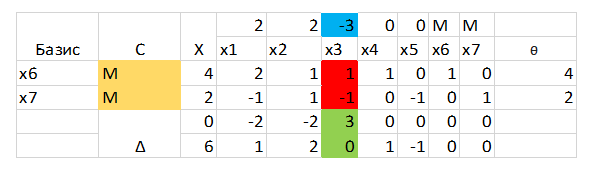
Дельта рассчитывается как: M*1+M*(-1)-(-3)=3+0*M. Коэффициент при М записываем в нижнюю строчку (то есть 0), без М – в верхнюю (то есть 3).
Теперь нам нужно выбрать максимальный положительный элемент из ∆, причем, если положительных нет (столбец Х в рассчет не идет), то мы нашли оптимальный план и ответом будут как раз коэффициенты в столбце Х с базисом текущим. Как мы ищем минимальную ∆?
Выпишем все ∆, что у нас есть: (-2+М),(-2+2М),(3),(М),(-М),(0),(0).
Очень просто, во-первых помним, что М – очень очень большое положительное число, то есть в рассчет могут идти только числа, где М>0 или, если М=0, то свободный член больше 0.
То есть в нашем случае из рассчета отбрасывается 5,6 и 7 элементы и остается список:
(-2+М),(-2+2М),(3),(М)
Теперь определим имеющиеся по порядку возрастания (делаю это раз, чтобы понятно было):
3<-2+M<M<-2+2M. Определяем порядок по коэффициентам при М, если они равны, то ставим меньшим то, где свободный коэффициент меньше.
Итого, мы нашли самый большой элемент, он оказался при х2. Выделим этот столбец – это и есть наш направляющий столбец.
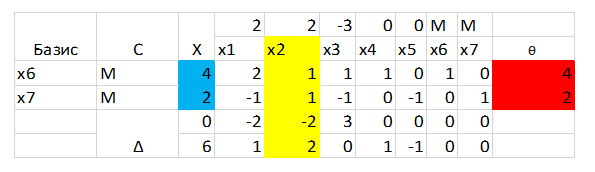
Направляющий столбец выделили желтым, теперь нужно рассчитать смещение θ, для этого делим элементы столбца Х на соответствующие им элементы из направляющего столбца, но, делаем это только в том случае, если в направляющем столбце элемент больше 0. То есть в нашем случае будет так: 4/1=4,2/1=2. Теперь нужно выбрать минимальное смещение, в нашем случае это 2 и эта строка становится направляющей. Выделим ее:
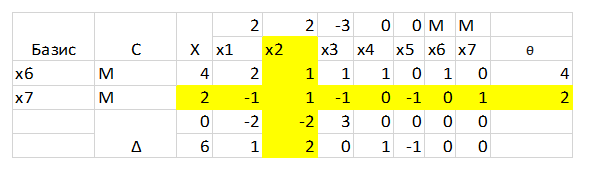
Итак, мы получили уже 2-й шаг по заполнению симплекс таблицы.
Дальше следует самая сложная часть, где нужно быть очень внимательным, а именно пересчет симплекс таблицы:
Выделяем направляющий элемент, он находится на пересечении желтой строки и желтого столбца. В нашем случае он равен 1. После чего делим все элементы направляющей строки на этот направляющий элемент. В данном случае направляющая строка никак не изменится (потому что делим на 1). После чего Для всех других строк (то есть, в данном случае, для первой), считаем по такому принципу: вычитаем из каждого элемента данной строки – произведение желтых элементов полученных, которые находятся в той же строке и столбце, что и изменяемая ячейка и разделить на направляющий элемент. Выпишу преобразования происходящие для первой строки:
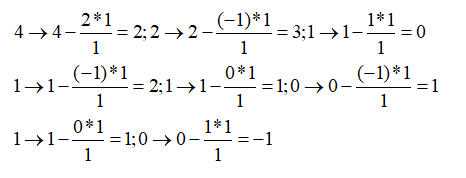
И выпишем уже пересчитанную таблицу:
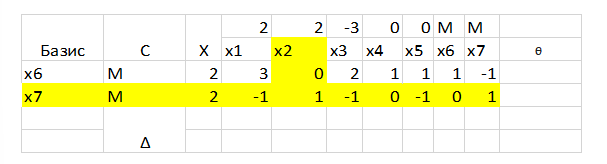
И остался последний шаг итерации, а именно вывод из базиса старой переменной и замены на новую. Это делает по такому принципу: выводим ту переменную, что находится в желтой строке и вводим ту, что находится в желтом столбце, то есть в данном случае выведется х7, а введется х2. При этом не забываем, что коэффициент в С меняется на тот, что находится при данной переменной в функции, то есть в данном случае при х2 у нас коэффициент 2, значит на него и будет замена.
Перепишем табличку с новыми выводами:
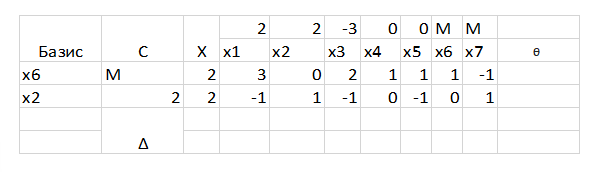
Чтож, все шаги понятны. А теперь все сначала =)
То есть рассчитываем оценки ∆:
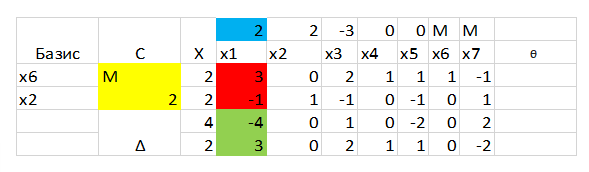
И, поскольку, у нас один из коэффициентов изменился, покажу еще раз, как рассчитывается оценка:
3*М+(-1)*2-2=-4+3М, что записывается -4 в верхнюю строчку дельты, а 3 при М – в нижнюю строчку.
Теперь выделим, какая из оценок максимальна, выпишем их ряд:
(-4+3М),(0),(1+2М),(М),(-2+М),(0),(2-2М)
Очевидно, что 2-й,6-й и 7-й элементы не подходят по причине отрицательности, итого у нас остается выбрать из:
(-4+3М),(1+2М),(М),(-2+М)
И из них максимальный элемент первый, а именно -4+3М, выделим этот направляющий столбец и подсчитаем θ:
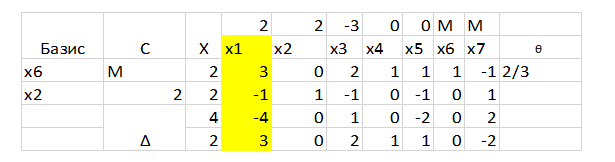
Первая строка считается очевидно: 2 из столбца Х и 3 из направляющего столбца. А вот вторая строка в рассчет не идет, поскольку элемент направляющего столбца, а именно -1, неположителен.
Итого, у нас очевидная направляющая строка, ведь выбор небогат)

Направляющий элемент у нас 3, чтож, значит разделим направляющую строку на него:
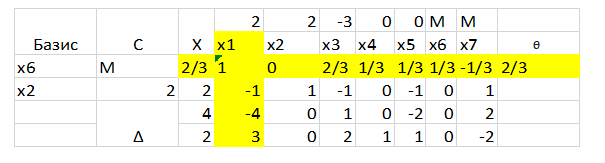
Теперь высчитаем другую строку (для базиса х2)
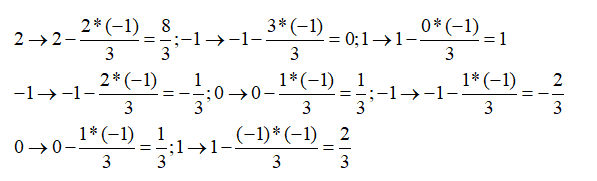
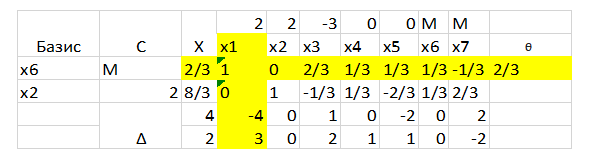
И последний шаг – выводим х6 и вводим х1.
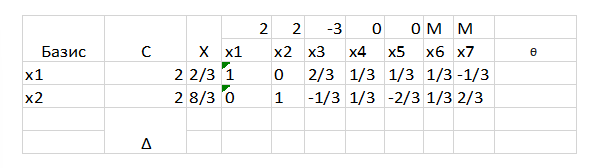
После чего, в принципе, можно избавиться от вспомогательных колоночек с х6 и х7, чтобы не считать их лишний раз, но я оставлю для наглядности и, чтобы, вы могли, если что, все проверить. На «чистовик» так подробно все не расписывается, а пишутся просто таблицы заполненные и пересчитанные с выделением на направляющих строках и столбцах, как будет далее. Забыл уточнить, в случае, если, у нас две ∆ получились одинаковыми – мы берем любую из них, какая больше по душе.
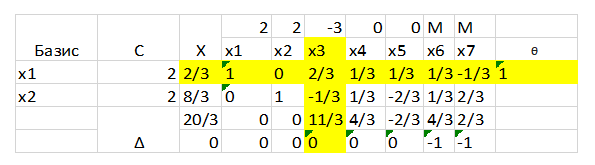
Выводим х1 и вводим х3
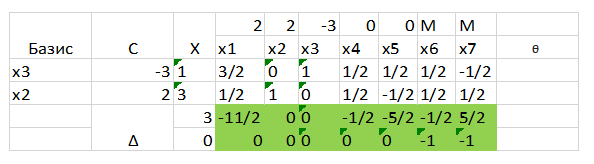
Как можно заметить – в зеленом поле все числа неположительны, а значит оптимальный базис был найден! Найти его можно в соотношении: столбца базиса и столбца Х. Попробуем подставить в исходное выражение эти числа (все х, что не вошли в базис приравниваются к 0):
Х1=0,Х2=3,Х3=1,Х4=0,Х5=0
F(0,3,1,0,0)=2*0+3*2+(-3)*1+0+0+1=1 и это минимум!
Попробуем подставить в уравнения ограничений:
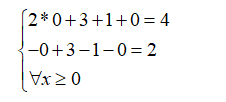
Магия да и только, но все сходится =)
Итого, 4-й пункт по решению задачи ручками мы решили, теперь можно написать программу, если поняли алгоритм)
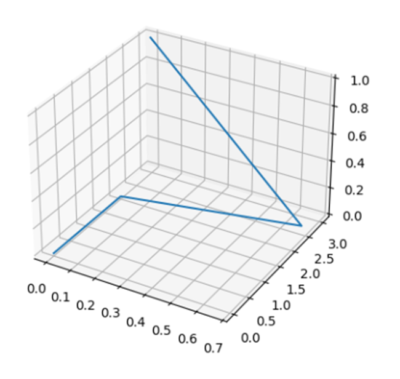
5-й пункт, построение графика, это делаете так: на каждой итерации талички отслеживаете не появились ли или не поменялись ли в базисе переменные х1,х2,х3, после чего по этим трем равным массивам можно построить трехмерный график их изменения.
Для этого пункта он получился таким:
Удачи в решении задач! Если будут какие-то вопросы, вы всегда можете написать мне в телеграм и задать их.
