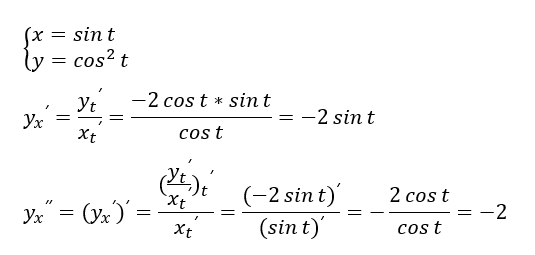Добрый день, граждане Империума! Сегодня мы разберем тему производных функции, а также несколько дополнительных примеров на применение. Тема эта, безусловно, очень полезная и обширная, что имеет множество граней и с которой вы еще не раз столкнетесь. На самом деле ничего в этой теме сложного нет, совершенно. Важно только быть аккуратным и внимательным, а там будете производные брать в уме.
Для начала стоит определиться, что дифференцирование и взятие производной связаны, но не одно и то же! Если хоть кто-то скажет, что это равноценные операции – будет мгновенное объявлен еретиком. А теперь разберем отличие (могут быть некоторые сложные слова, для общего понимания их знать не обязательно):
Дифференциал – фундаментальное деление исчислений на бесконечно малых изменениях (то есть дифференциальное исчисление, есть так же интегральное исчисление, что будет в будущих статьях разобрано)
Производная – функция, что является результатом применения к исходной функции операции дифференцирования.
То есть можно сказать, что:
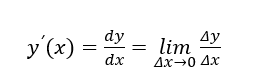
тут последнее равенство означает бесконечно малое приращение. Если будет интересно – дайте знать, разберу подробнее эту тему 😉
А теперь как, собственно, брать производные. Для начала вот табличка, ее нужно запомнить наизусть, либо уметь выводить. Но помнить ее нужно лучше, чем имена 18 примархов!
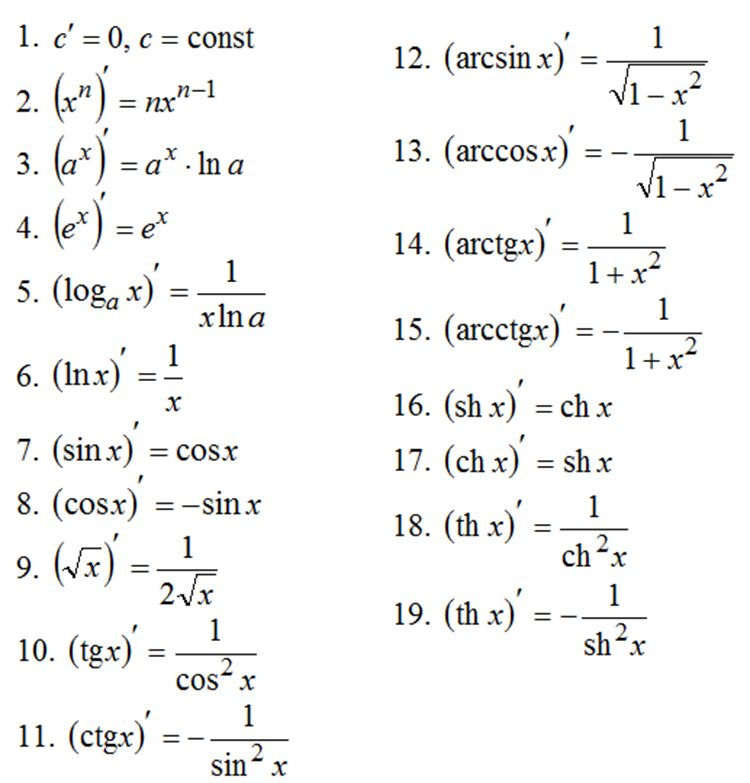
Операции с производными проводятся по принципу от внешних к внутренним, а арифметические по законам ниже:
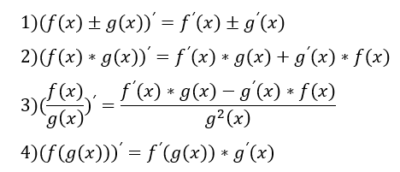
А теперь разберем это все на примере, который я распишу в деталях:
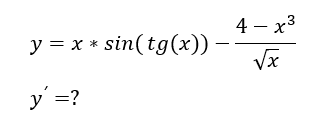
Начнем его разбивать мысленно по кусочкам, от которых можно будет легко взять производную, разбивать будем по законам, расписанным выше.
Первый шаг очевиден, по первому правилу разбиваем:
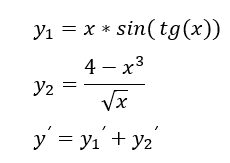
Далее видно, что в y1 нас умножение, то есть второе правило применяется:
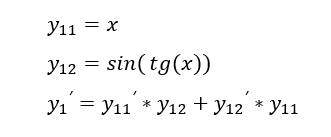
А в y2 деление, то есть применяется третье правило:
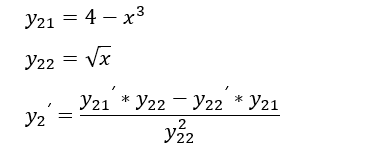
Уже сейчас можно заметить, что производные от y11 и y22 – это табличные производные и дальше их расписывать не требуется) А вот другие два нуждаются в дальнейшей «обработке».
Первый наш член – это y12, который распишем по правилу 4, по-другому это называется производная сложной функции:
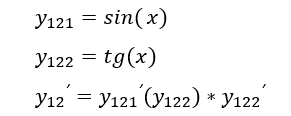
И вот мы разбили до еще двух табличных значений, остался последний, y21, а его разбиваем по уже известному первому правилу:
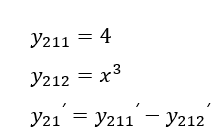
Понимаю, что тяжело, но уже финишная прямая, возьмем производные от всех простых функций:
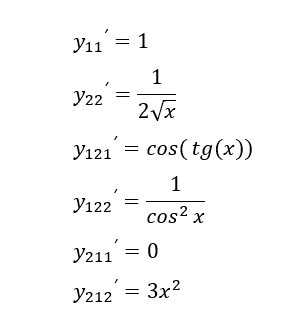
Из них соберем последовательно более сложные выражения:
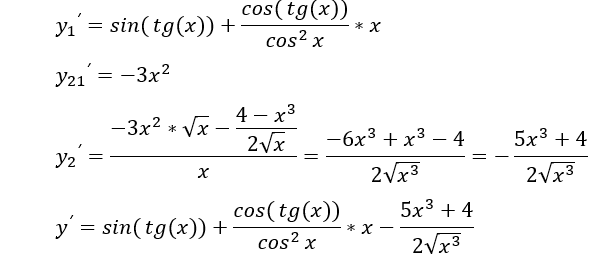
Ура, поздравляю, мы все посчитали)
Теперь разберем несколько типовых задач с применением производных:
- Правило Лопиталя, когда не берется предел нормальным способом, но он имеет неопределенность вида 0/0 или inf/inf
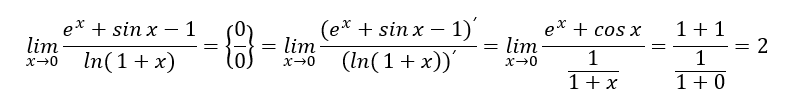
Бывает сложнее, если функция вида xx, но в этом случае можно просто прологарифмировать, как в дальнейшем примере:
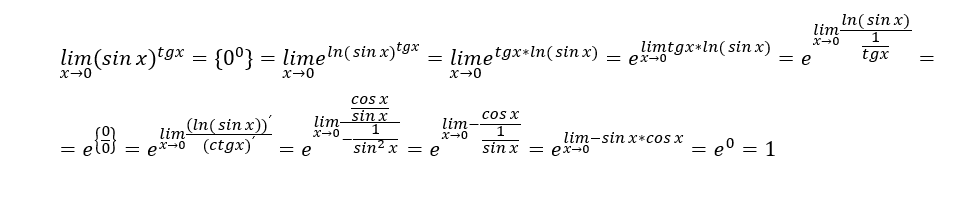
2. Взятие производной у функции заданной неявно, тут все тоже очень просто, достаточно принять y за сложную функцию и не «сокращать» ее производную, после чего перенести все с ней в одну часть, вынести за скобки и разделить. Лучше разберем на примере:
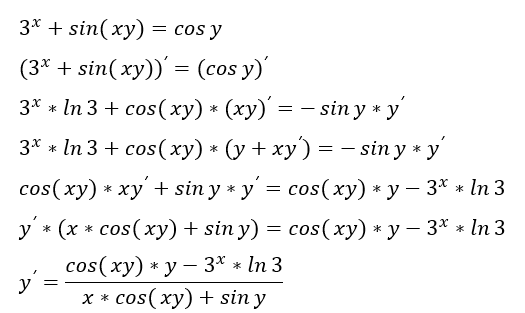
Как видите, все просто и элементарно) Не стоит бояться таких примеров. Ах да, напомню, если будут непонятные моменты – вы всегда можете написать апелляцию в нашего бота в контактах или связаться напрямую в телеграмме @The_GodEmperor
3. Ну, например, иногда может понадобиться взять производную от системы, разберем разные варианты таких слаанешитских извращений: